Rules occupy a hazy area between data and procedure. Like data, each rule in a rule base is independent, and can be linked to other rules dynamically based on common values. Like procedures, each rule has multiple substatements specifying conditions and/or actions related to the execution or firing of the rule.
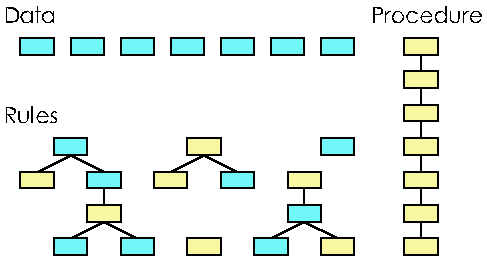
Looking at it another way, both databases and procedures can be thought of as degenerate cases of rule bases. A database is a collection of rules that have no action statements and only one set of conditions. A procedure is one big rule with many statements. Figure 1 illustrates the relationship between data, procedure and rules.

Figure 1: The relationship between data, procedure and rules.
Because most programming tools are designed for either data or procedures, when confronted with a specification written as a collection of rules, the developer is faced with a tricky problem. The rules cannot be expressed in data, and coding them procedurally leads to spaghetti code for even the best of programmers. Further the original rules get lost in the code, become difficult to debug, and almost impossible to update if necessary.
Ironically, this difficult part of an application is often its heart, and, to make matters worse, the piece most likely to change.
Consider a billing application for a phone company. Most of the application is cleanly coded using data for calls and customers, and procedures for processing the data. But pricing the call is the tricky part, based on a collection of rules derived from marketing concerns, local regulations, various sub-carriers, and special arrangements with large customers, all on top of the expected rules based on time-of-day, physical distance of call, length of call, and whether it was a credit card, collect or directly billed call.
All you need to do to understand the importance of phone call pricing is listen to the large phone company's ads. Each claims to have better pricing rules. The volatility of the rules derives from the competitive environment, evolving technology and changing government regulations.
The phenomena of a difficult rule-based component being the heart and soul of an otherwise straight-forward application occurs over and over. Consider the underwriting rules for insurance companies, the scheduling rules for an airline, the configuration rules for manufacturing, the diagnostic rules in a help desk, loan approval rules in banking, and exception handling rules in process control.
So what's a programmer to do? There are tools for coding rules directly, but there are two major problems with them, one related to environment and the other to the rule language itself.
The environment issue is simply one of integration. Most of an application can be implementented using conventional database and programming tools. To be practical, the rule-based component must easily become a part of the full application architecture.
The rule language issue is a more difficult one. The sad truth is the rules for one problem domain are not really very much like the rules for another. It is simply not clear what a universal rule language should like. If a rule language is easy to use, then the chances are it doesn't have the power or expressibility necessary for very many application areas. If a rule language has all of the bells and whistles necessary for multiple application areas, it becomes very difficult to use.
Because of these difficulties, most programmers simply roll up their sleeves and start forcing the rules into procedural code. It is for this reason that few applications really have any heart.
There is another option, and that is to build a custom rule-engine for the application. The custom rule-engine uses a rule syntax that mates well with the problem domain, provides integration tools directly related to the application, and processes the rules in the most sensible manner.
The design issues with rule engines are not dissimilar from the issues with data engines. That is, for a program to access data two things need to happen. One, a format for the data needs to be designed, and two, software that accesses the data needs to be designed.
This is true for both external data bases, which range from simple flat files to full relational systems, and internal data that can be represented in arrays, structures, linked lists or arbitrarily complex combinations of all three. In each case the programmer picks a representation and uses either canned software or writes some new code to handle the data.
Rules present the same technical challenges. A format for the rules needs to be designed, and software that provides accesses to the rules needs to be provided. As with data, there are many possibilities, depending on the situation.
The format of the rules is, of course, the rule language. It typically has rules expressed in an 'if-then' syntax, but because the way the 'if' side of the rule relates to the 'then' side of the rule, the more general terms 'left hand side (LHS)' and 'right hand side (RHS)' are often used.
The rules refer to data represented in some manner. The rule engine decides, based on the data, which rules to activate and in what order. The results of picking one rule will dictate which rule follows. Thus the execution order of the rules is determined dynamically, and is a function of the data fed to the rule base.
Three key technologies are needed for implementing a rule engine.
While these tools can be developed in any language, they are an integral part of the Prolog language. For this reason Prolog is used for the sample code in this article. The design ideas, however, are not language dependent and can be implemented in any language. (I've seen rule languages implemented in C, Smalltalk, Pascal, Lisp, and even COBOL.) But, given an efficient implementation of Prolog that can also be embedded in other languages, Prolog becomes an excellent tool for implementing customized rule engines designed to be components of larger systems.
Given that rule-based components of applications often need to be easily read and maintained, a major goal of rule design is to reduce the 'semantic gap' between the expression of the rules in the problem domain and the code for the rules.
One of the biggest problems with coding rules procedurally is the code no longer looks like the rules. It is difficult to see the rules in the code, and more difficult to modify or add new rules to the code. (The situation is very similar to that encountered years ago when programmers were forced to code scientific equations in assembler. The large semantic gap between the specification of an equation and the code that implemented it made the code unreadable in terms of the application's purpose. Languages such as FORTRAN narrowed the semantic gap making it much easier to build and maintain programs with equations in them.)
For example, we implemented a system that set the myriad installation parameters required for installing a large complex IBM mainframe software product. The field support people were used to working with printed documentation that specified the relationships between components of the software, and the settings for various parameters. That documentation looked very much like the following rule from the automated system.
quest loadunit default @ diskunit edit none prompt [‘What is the unit for the load library?’].
What is of interest here is the @ sign. For the installers it had a specific meaning, which is that this parameter defaults to the same value as another parameter. Using a generic rule language, the information in this rule would probably require using if-then syntax rules, something like this.
if parameter = loadunit and no_value_specified then get_value(diskunit, X) and set_value(loadunit, X).
The custom rule engine, by contrast, supports a rule language that is very close to the way the engineers think of the rules, and automatically applies the rules as expected. The result is a rule language that is much more readily accessible to both the designers of the rules and the users of the rules.
That same application also required reasoning about the interrelationship between products. Again, a custom representation was used that did not require an if-then syntax. The following rule specifies the relationship between products, and the rule engine applies these rules in the correct way.
product ‘ADS Batch 10.1’ password [adsb] corequisites [‘IDMS DB’, ‘IDD’].
There were some if-then rules as well in this application, but a large percentage of the potential rules were eliminated through the use of a customized syntax for expressing the rules and a customized rule engine that applied the rules.
Rules always express relationships between data elements. One key design question is how is the data represented? The simplest approach is attribute value pairs, as shown in the automobile driving advisor in Example 1. It uses, for example, the attribute 'traffic_light' which can have various color values.
if traffic_light is green then action is proceed. if traffic_light is red then action is stop. if traffic_light is yellow and driving is crazy then action is accelerate. if traffic_light is yellow and driving is sane then action is stop. if city is 'Boston' then driving is crazy. if city is not 'Boston' then driving is sane.
Example 1: Rules advising an automobile driver.
Attributes and their values can be easily represented using Prolog's built-in database tools. For example, if the color of the traffic light was determined to be red, this Prolog statement would execute:
assert( known(traffic_light, red) ).
The pattern-matcher, when deciding if a rule should fire, poses Prolog queries, such as:
known(traffic_light, green).
The simple attribute-value idea can be extended to allow attribute-value pairs to be associated with objects, as in 'car_1 color is red'. That idea can be further expanded into more complex data representations, such as frames. Frames are a very powerful way of representing data that incorporates many of the same ideas as OOP, including the ability to set default values, inherit from other frames, and transparently contain procedures for calculating values. They can also contain deamon procedures that are triggered by changes to frame attributes or slots.
The data representation in the installation application described in the previous section is a simple frame-like representation. Each frame contains 'slots', that, in the example, represent the name of the object, the default value, the edit criteria, and the prompt to be given to the user if necessary.
Some applications benefit from these more complex schemes and others have no need for them. The installation system needed more complex data representation because much of the knowledge in the system was more naturally expressed as data relationships.
In many cases the rules depend on data that is acquired from the user, by asking. In this case the rule engine needs to remember the answers to questions and only ask the first time a rule needs to know something from the user. For example, four of the driving advisor rules in Example 1, need to check the color of the light. The user would get aggravated if the system asked the user each time it tested a rule.
The Prolog code in Example 2 can be used by an engine to ask and remember. It uses two Prolog rules. The first checks to see if an attribute already has a known value, and, if so compares it to the required value and either succeeds or fails. If there is no previous known value, then the second rule fires, asking the user, saving the answer and again checking to see if the answer was as expected.
(Prolog note: terms beginning with upper case letters are variables.)
ask(Attr, Val) :- known(Attr, X), !, X = Val. ask(Attr, Val) :- write(‘What is the value of ‘), write(Attr), read(X), assert( known( Attr, X ) ), X = Val.
Example 2: Prolog code that 'ask's a user for the value of an attribute, and remembers the answer for future queries.
As the rule engine starts to look for rules it will need to ask the user about the color of the light. It will only ask once, and when testing other rules will use the remembered answer to the question. The value of city will only be asked for if it is needed. That is, unless the user indicates the light is yellow, the rule engine will never need to find out the value of city.
This type of user interaction is particularly important for diagnostic systems, where the system is trying to determine the cause of a problem based on a dialog with the user. By using a predicate such as 'ask' a system can be designed to only ask questions that are triggered by pertinent rules, and only ask when the data is actually needed.
Stand-alone rule-based systems have the luxury of having their own self-contained data representation. Component rule-base systems, on the other hand, might need to gather data outside of the rule base.
In this case the system can be designed so that data external to the rule base is gathered to populate internal data, or it can be designed so that the rules directly reference external data. In the first case, the system is designed so that the caller provides the required information. In the second case the rule engine must be designed to provide the rule base with access to external information.
For example, a system that prices telephone calls has no need for user interaction. Instead, it must gather its data from the database, getting particulars on the call, the customer, the carrier, and other relevant information.
A component rule-base might also need to gather information from external procedures. A rule-base concerned with monitoring physical processes or hardware needs to access functions that provide information about the process or hardware in question.
For each of these cases, a predicate similar to 'ask' is written that either goes to the database or some external function to get the information required for the rules.
Different types of problem domains require different types of reasoning support. For example a system that is concerned with monitoring physical processes needs to be able to include rules that reason over time. The concepts of before and after need to be part of the rule language. The same is true of scheduling systems.
Similarly, systems that configure physical components, such as laying out circuit boards, need to be able to express spatial relationships.
The same considerations apply to smaller details that can make a rule language more accessible. Consider the telephone call pricing system. It needs to have a clear and easy way of representing just the area code and/or exchange of a phone number, for use in various rules and database queries. This is not a difficult feature to add, but one that makes the coded rules that much easier to read for those non-programmers that make the rules.
The defining aspect of any rule engine is the way it dynamically links rules together. There are two fundamentally different approaches, goal-driven, sometimes called backward-chaining, and data-driven, sometimes called forward-chaining.
Goal-driven rules are more common. They are written with the idea that each rule defines a goal to be satisfied, and the subgoals that make it true. This approach is typically used for diagnostic-type systems and identification systems.
The call pricing system falls in this category. There are rules that determine call price which are dependent on sub-rules that determine the carriers used, the local regulations, etc. etc.
The Example 1 driving advisor is the same. The system starts with the goal of determining the action to take, and then proceeds to the subgoals of finding the color of the light, and if necessary the city.
Because goal driven rules can be neatly organized according to goals and subgoals, and because people often think of problems in those terms, goal-driven rules are popular for many applications.
Prolog is itself a goal-driven rule-based language. A basic Prolog rule is of the form:
goal(X, Y) :- sub_goal_one(X), sub_goal_two(Y).
Because Prolog is a rule-based language, it can be used directly for many rule-based applications. Often pure Prolog rules with a few helper predicates, such as 'ask' introduced earlier, will be adequate for building a rule-based component.
Example 3 shows the driving advisor written in pure Prolog, with the help of 'ask'. To use it, one simply poses the Prolog query 'action(X)'. After 'ask'ing one or two questions, X will be bound to the answer.
action(stop) :- traffic_light(red).
action(proceed) :- traffic_light(green).
action(accelerate) :- traffic_light(yellow), driving(crazy).
action(stop) :- traffic_light(yellow), driving(sane).
driving(crazy) :- city('Boston').
driving(sane) :- not city('Boston').
traffic_light(X) :- ask(traffic_light, X).
city(X) :- ask(city, X).
Example 3: The driving advisor in pure Prolog.
Because this article is about building rule engines, Example 4 shows a four-rule Prolog program that implements a basic Prolog interpreter in Prolog, as well as supports the special predicate 'ask'. It can be used with the rules in Example 3 as easily as the real Prolog interpreter. Simply pose the Prolog query 'prove(action(X))' to get the value of X.
prove(true) :- !.
prove(ask(A,V)) :-
!, ask(A,V).
prove((Goal,Rest)) :-
prove(Goal),
prove(Rest).
prove(Goal) :-
clause(Goal, Body),
prove(Body).
Example 4: A Prolog interpreter in Prolog.
The four Prolog rules in Example 4 say:
1) If the goal is the atom true, then we've reached the end of the proof. (Facts, rules with no bodies, always end in true. For example, the fact 'sky(blue).' is really stored as the degenerate rule 'sky(blue) :- true.')
2) If the goal is 'ask', then call ask directly. This is needed as a special case because usually the rules for the rule engine, including 'ask', will be compiled, and not dynamically stored.
3) If the goal is a comma-delimited list, prove the first goal in the list and then prove the rest of the list.
4) If the goal is a single goal, then see if there is a rule (clause) in the database who's head unifies with the goal, and if so, get its body. Then prove the body.
Prolog unification automatically takes care of pattern-matching between goals and the subgoals of rules. Prolog search will cause all of the rules (clauses) to be tried in an effort to prove a goal true or false. Prolog recursion will carry the search to whatever depth of nesting is required.
Given this template, it is easy to modify this scheme to come up with custom variations on both Prolog inferencing and rule representation. Consider again the rules in Example 1. The Prolog code in Example 5 will interpret those rules exactly as they are written.
The operator definitions in Example 5, starting with ':- op', tell Prolog to accept terms such as 'pred(arg1, arg2)' when written as 'arg1 pred arg2'. This is how Prolog accepts the natural looking rule syntax of Example 1.
:- op(790, fx, if). :- op(780, xfx, then). :- op(770, xfy, and). :- op(700, xfx, is). :- op(690, fx, not). prove( Attr is Value and Rest ) :- getav(Attr, Value), prove(Rest). prove( Attr is not Value) :- atomic(Value), not(ask(Attr, Value)). prove( Attr is Value) :- getav(Attr, Value). getav( Attr, Value ) :- if Conditions then Attr is Value, prove( Conditions ). getav( Attr, Value) :- not(if _ then Attr is _), ask( Attr, Value ).
Example 5: Rule engine for Example 1 rules.
The rules of 'prove' cover three cases. 1) If there is a list of subgoals to prove, separated by 'and's, then call getav to see if the first attribute value pair is true, and, if so, prove the rest. 2) If there is a single negated goal, simply ask for the value and negate it. 3) If there is a single goal, call getav to see if its true.
The rules of 'getav' cover two cases. 1) If the attribute is defined in the 'then' side of a rule, try to prove the 'if' conditions of the rule. 2) If the attribute is not on the 'then' side of any rule, its OK to ask the user.
Again, Prolog recursion, unification and backtracking do most of the work. To use this rule engine, simply pose the Prolog query 'prove(action is X)', and, just as in the other cases, X will wind bound to the answer.
Data-driven rules are often called production or rewrite rules. The 'if' side of the rule refers to data that is known to the system. If the data in the system matches the pattern on the 'if' side, then the rule is said to be fireable. Firing the rule means the actions on the 'then' side of the rule are taken. These actions change the state of the known data, often adding assertions, thus making other rules eligible to fire, and the cycle continues.
Data-driven rules can be more difficult to work with, but they allow for rule-based expressions of complex configuration-type applications that cannot be easily implemented with goal-driven rules. They start with the initial data of the system to be configured, transform it to a new state which is further transformed until a final configuration is reached.
This type of problem does not code well with goal-driven rules because the final goals cannot be easily ennumerated. For example a scheduling system can produce an infinite variety of schedules, depending on the input data. Contrast this to a diagnostic system, which will always be diagnosing the same finite set of problems.
Even though Prolog is a goal-driven language, it can be used to implement a data-driven rule engine as easily as it implements a goal-driven one.
Example 6 shows one rule from a sample data-driven system that configures living room furniture. The system starts by asking the user the dimensions of the room and the list of furniture to be configured. The rules gradually transform that data until no more furniture can be placed in the room.
The rule shown places the TV opposite the couch. It will only fire when a couch is already in position, there is a TV that has not been placed, and there is enough room on the wall opposite the couch to hold the TV. (Note the use of the spacial predicate, opposite.)
When it does fire it removes the TV from the unplaced list, positions the TV on the opposite wall from the couch, and updates the space available on that wall.
rule f3:
[1: furniture(tv,LenTV),
2: position(couch, CW),
3: opposite(CW, W),
4: wall(W, LenW),
LenW >= LenTV]
==>
[retract(furniture(tv, LenTV)),
assert(position(tv, W)),
retract(wall(W,LenW)),
NewSpace = LenW - LenTV,
assert(wall(W, NewSpace))].
Example 6: A sample data-driven configuration rule.
Example 7 shows the essential parts of a rule engine that interprets data-driven rules. It uses Prolog operators, like the goal-driven rule engine, to allow for a readable presentation of the rules.
The main predicate, 'go', finds a rule, tests to see if the left hand side of the rule matches the known facts at the time, and, if so performs the actions on the right hand side. It then repeats the cycle by recursively calling itself.
The 'match' predicate walks the list of conditions, either comparing each with the known facts or performing indicated tests. The 'process' predicate walks the list of actions, taking each in its turn.
go :- rule ID: LHS ==> RHS, match(LHS), process(LHS, RHS), !, go. go. match([]) :- !. match([N:Prem|Rest]) :- (fact(Prem); test(Prem)), match(Rest). test(X>Y) :- X>Y,!. test(X>=Y) :- X>=Y,!. process([],_) :- !. process([Action|Rest],LHS) :- take(Action,LHS), !, process(Rest,LHS). take(retract(X)) :- retract(fact(X)), !. take(assert(X)) :- asserta(fact(X)), !. take(X = Y) :- X is Y, !. take(write(X)) :- write(X),!.
Example 7: A data-driven rule engine.
This basic program can be modified and expanded to handle any degree of added sophistication one might want to add to the rule-engine, and there are plenty of wrinkles that can be added to a data-driven rule engine, including full frame-based representation of knowledge and various rule indexing schemes to improve search performance for large rule bases.
Some rule-based systems produce definitive results. Phone call pricing is one example. Others deal with fuzzier situations and need to quantify the probability of the possible answers. Diagnostic systems sometimes fall into this category.
In these cases the rule engine must be designed to carry probabilities along with various conclusions, and propagate those probabilities through linked rules and data.
This type of extension can be added to the rule engines shown so far by simply carrying an extra argument representing uncertainty. The formula for propagating that uncertainty becomes part of the rule engine, as does some criteria of minimum certainty required to continue a proof.
Example 8 shows some automobile diagnostic rules that include 'certainty factors', represented by cf. These are a simple, pseudo-probabilistic way of representing certainty on a scale of 0 to 100.
rule 1
if not turn_over and
battery_bad
then problem is battery cf 100.
rule 2
if lights_weak
then battery_bad cf 50.
rule 3
if radio_weak
then battery_bad cf 50.
rule 4
if turn_over and
smell_gas
then problem is flooded cf 80.
Example 8: Rules with uncertainty.
Most rule-based systems are simply required to produce an answer, but some systems are required to explain themselves as well. This might be because the system is providing advice that may or may not be taken by the user, or it might be because the system is used in a training capacity as well. Explanations are also invaluable for the system developers to use as a debugging aid.
Explanations are usually presented in the form of rule traces, but other more complex schemes can be implemented as well. In any case, the explanation facility is just one more extention that can be added to the rule engines presented so far.
In the preceding examples rules were represented as Prolog terms, made more readable through the use of Prolog operators. Sometimes, however, a more general purpose syntax is required.
Prolog provides for this with a built-in parser called Definite Clause Grammar (DCG). It allows you to specify language rules, and also translate the language into pure Prolog terms.
For example, the rules in Example 8 are not defined with operators, but are translated by DCG rules into formal Prolog syntax. The formal representation of the fourth rule of Example 8 is:
rule(4, lhs([av(turn_over,yes), av(smell_gas,yes)]), rhs(av(problem, flooded))).
The rule engine uses this formal syntax. Some of the DCG rules that transform the rules are shown in Example 9. Note that the grammar rules allow multiple ways of representing an attribute value pair. Either 'is' or 'are' can be used, and if only a single word is encountered, it is assumed to mean the attribute only has a yes or no value.
The grammar rules assume that each rule was first read into a Prolog list of words, such as [rule, 3, if, radio_weak, then, battery_bad, cf, 50]. (The bracketed items in the grammar rules are picking out the reserved words in the diagnostic rules. As always, an initial upper case letter indicates a variable.)